탐욕 알고리즘 { 호프만 트리 }
탐욕(Greedy) 알고리즘: 각 단계의 부분 문제를 풀 때 매 선택에서 지금 이 순간 당장 최적인 답을 선택하여
적합한 결과를 도출한다고 해서 붙여진 이름.
동적 계획법 보다 효율적이기는 하지만 반드시 최적해를 구해준다는 보장은 하지 못한다.
대상 문제가 최적 부분 구조를 가지고 있어야 한다.
동작 순서
1) 해 선택: 현재 상태에서 부분 문제의 최적해를 구한 뒤 이를 부분해 집합에 추가함.
2) 실행 가능성 검사: 새로운 부분해 집합이 실행 가능한 것인지 확인. 문제의 제약 조건을 위반하지 않았는지 검사하는 것.
3) 해 검사: 새로운 부분해 집합이 문제의 해가 되는지 확인. 전체 문제의 해가 완성되지 않았다면 1단계부터 다시 시작.
고정 길이 코드: 모든 코드의 길이가 똑같은 값을 갖는 코드 체계를 말한다. 자주 사용하는 ASCII 코드가 예시이고 최대 장점은
다루기 쉽다는 점이다.
가변 길이 코드: 저장 공간을 절약하기 위해 사용하는데 데이터 처리가 상당히 번거롭다는 단점이 있다.
접두어 코드: 가변 길이 코드의 한 종류, 무 접두어 코드라고도 불리는데
코드의 집합의 어느 코드도 다른 코드의 접두어가 되지 않는 코드
ex) {0,1,01,010} 은 접두어 코드가 아니다. 0과 1이 01과 010의 접두어가 되기 때문.
{00,010,100,101}은 어느 코드도 다른 코드의 접두어가 되지 않기 때문에 접두어 코드라고 할 수 있음.
기호의 빈도: 한 기호가 데이터 안에서 차지하는 비율. ex) Apple의 경우 p는 2, A와 l , e는 빈도 1을 가짐.
길이가 짧은 접두어 코드를 빈도가 높은 기호에 부여하기 위해 사용하는데 이렇게 하면 저장 공간을 아낄 수 있기 때문이다.

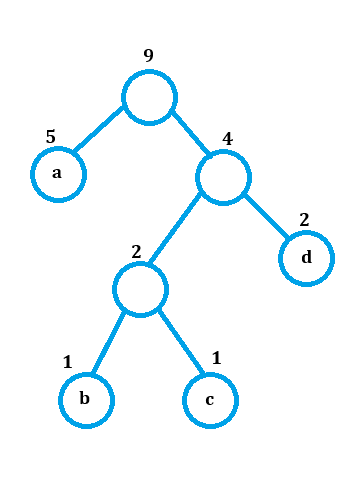
허프만 트리: 트리의 노드에서 왼쪽 자식 노드는 0, 오른쪽 자식 노드는 1을 나타내고 모든 기호는 잎 노드에만
기록할 수 있다, 뿌리부터 잎의 경로가 기호의 접두어 코드가 되는데 이런 방식으로 표현한 이진트리를 허프만 트리라고 한다.
ex) 그림에서 a는 0 , b는 100, c는 101, d는 11이 됨.
경로가 길어질수록 접두어 코드 역시 길어진다.
빈도가 높은 기호일수록 경로를 짧게, 빈도가 낮은 기호일수록 경로를 길게 가져가야 압축률이 높아진다.
이렇게 압축률이 높게 만들려면 탐욕 알고리즘 3단계를 적용하면서 트리를 구축하면 된다.
해 선택 - 실행 가능성 검사 - 해 검사
- 각 문자와 빈도수(가중치)를 노드로 만듦.
- 가장 빈도수가 낮은 두 노드를 선택.
- 그 둘을 부모 노드로 합쳐서 새로운 노드 생성 (가중치는 합).
- 새 노드를 다시 트리에 삽입.
- 트리에 노드가 하나만 남을 때까지 반복.
데이터 압축
문자열 'aabbcdd'를 허프만 트리가 나타내는 해당 문자의 접두어 코드로 변환하면 압축이 된다.
0 0 100 100 101 11 11로 압축이 된다. ASCII라면 56비트일 크기를 15비트로 압축함.
데이터 압축 해제
비트를 읽을 때마다 잎 노드를 만나기 전까지 노드를 순회하면 된다.
잎 노드를 만나면 해당 기호를 버퍼에 넣고 뿌리 노드로 돌아간다
허프만 트리와 압축 해제된 데이터를 담는 용도로 사용할 버퍼를 준비함.
방금 압축한 001001001011111을 복원해 볼 것이다.

ex) 순서대로 읽기 시작 00은 바로 aa
1은 잎을 만나지 못해서 다음 0으로 이동, 여기서도 못 만나서 0으로 이동 => b를 넣음 aab
다음 100 역시 b를 넣기에 aabb, 그다음 101은 c여서 aabbc, 11은 d이기에 2번을 넣으면 aabbcdd로 복원 완료.