알고리즘 성능 측정 기준
1. 정확성 - 알고리즘이 입력 값에 대해 정해진 절차를 수행하여 결과적으로 정확한 출력을 제공하는가를 가리키는 기준.
2. 작업량 - 요구되는 기능을 수행하기 위해 알고리즘이 수행해야 하는 작업의 양이 얼마나 되는가를 가리키는 기준.
3. 메모리 사용량 - 해당 알고리즘이 작업을 수행할 때 사용해야 하는 메모리의 양을 의미.
4. 단순성 - 복잡하면 개선과 분석이 어렵기 때문에 중요한 요소.
5. 최적성 - 더 이상 개선할 부분이 없을 정도로 최적화되어 있는가를 가리키는 기준.
알고리즘 수행 시간: 알고리즘이 입력을 받아 실행되었을때, 해당 입력을 처리하는 데 걸리는 시간. 실제 시간을 측정하는 것은
제약이 많기에 입력 크기에 따라 시간이 얼마나 증가하는가를 보는 시간복잡도를 사용하고 최악과 최선, 평균을 찾는게 목표이다.
점근 표기법: 시간 복잡도를 수학적으로 간단하게 표현하기 위한 표기 방식.
알고리즘의 성능차이는 대규모 데이터를 다룰 때 더욱 두드러지는데 무한대에 가까워질수록 차이가 분명해진다.
데이터의 크기가 커질수록 최고차항을 제외한 나머지 항의 영향은 거의 없다.
그래서 점근 표기법에서는 최고차 항을 제외한 모든항과 모든 계수를 제거한다.
알고리즘 성능을 단순화하여서 알고리즘 간 성능 비교가 용이하다.
점근 표기법 3가지
O(Big O) 표기법 - 최악의 경우 알고리즘 수행시간을 나타내고 가장 많이 사용하는 알고리즘 성능 표기법이다.
대문자 O를 쓰고 그 옆에 괄호를 열고 닫은 후 그 안에 증가함수를 넣는 방법으로 사용한다.
증가함수란 입력 데이터의 크기 n에 대해 알고리즘의 수행 시간이 늘어나는 비율을 나타내는 함수이다.
ex) 최대 수행 시간이 2n^2 + 4n인 알고리즘 일 때 최고차 항을 제외한 모든 항과 계수를 제거하면
n^2 가 증가함수가 남고 이를 O(n^2)로 표현.
이때 O(n^2)는 이 알고리즘은 최대 n^2까지 걸리지만 그 이상은 아니다.
O(n^2) 보다 연산 횟수가 작은 모든 함수들의 집합이다. 빠른 함수들이 느린 함수 집합에 포함된다. 최대 ~만큼 걸리는 상한선 개념.
Ω(Big Omega) 표기법 - 최선의 경우 알고리즘 수행 시간을 나타낸다. O표기법의 반대.
ex) 최선의 경우 증가함수가 3n^2 + 8n일때 Ω(n^2)로 표현.
이때는 느린함수들이 빠른 함수 집합에 포함되는데 최소 ~만큼 걸리는 하한선의 개념.
Θ(Big Theta) 표기법 - O표기법과 Ω표기법을 모두 만족시키는 증가함수를 나타내는데 O표기법과 Ω표기법의 교집합이라고 할 수 있음. 시간복잡도는 정확하게 이 정도이다라는 의미.
요약
O표기법은 점근적 증가율이 자신의 증가함수를 넘어서지 않은 모든 증가함수를 포함.
Ω표기법은 점근적 증가율이 자신의 증가함수보다 작지 않은 모든 증가함수를 포함.
Θ표기법은 점근적 증가율이 자신과 같은 증가함수 만 포함.
재귀 방정식: 자기 자신을 항으로 갖는 방정식. 재귀 알고리즘의 성능을 나타낼 때 사용하는 방식.
팩토리얼: 1부터 양의 정수 n사이의 모든 정수를 곱하는 것으로 n! 형태로 표현한다.
n! = nx(n-1)!이고 다시 (n-1)!은 (n-1) x (n-2)!로 표현이 가능하다.
이런 성질을 이용하여 팩토리얼을 재귀 방정식으로 나타내면 다음과 같다.
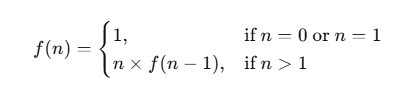
하지만 재귀 방정식을 사용해서 알고리즘을 성능을 알아내려면 복잡하고 어렵다는 단점이 있다.
마스터 정리: 이러한 재귀 방정식을 쉽게 해결해주는 공식.
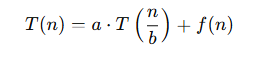
- a: 부분 문제의 개수
- n/b: 부분 문제의 크기
- f(n): 분할 후의 추가 작업 시간 (분할, 병합 등)
a, b, f(n)이 가진 값을 계산해서 f(n)이 n^{ log_b a} 보다 작은지/같은지/큰 지에 따라서 Case가 결정되고 케이스 별로
시간 복잡도가 도출됨.
Case 1- f(n)이 n^{ log_b a} 보다 작을 때, T(n) = Θ(n^{log_b a})
Case 2- f(n)이 n^{ log_b a}과 같을 때, T(n) = Θ(n^{log_b a}*log n)
Case3 - f(n)이 n^{ log_b a}보다 클 때, T(n) = Θ(f(n))
'자료구조' 카테고리의 다른 글
| 동적 계획법 { LCS 알고리즘} (0) | 2025.04.24 |
|---|---|
| 분할 정복 알고리즘 {병합 정렬, 거듭 제곱 계산, 피보나치 수 구하기 } (0) | 2025.04.24 |
| 문자열 탐색 알고리즘 {라빈-카프, KMP, 보이어 - 무어} (0) | 2025.04.23 |
| 그래프 (0) | 2025.04.22 |
| 해시 테이블 (0) | 2025.04.22 |



